What is mensuration

 

MENSURATION

क्षेत्रमिति (क्षेत्रफल - Area)

1. क्षेत्रमिति की परिचय बताये है ?

क्षेत्रमिति में परिमिति, क्षेत्रफल, आयतन, आदि की माप के बारे में अध्ययन किया जाता है। और इससे जुड़े सवाल आपको प्रायः प्रत्येक प्रतियोगी परीक्षा में जरुर पूछा जाता हैं।
☆ यदि किसी आयत के आसन्न भुजाओं में एक को शांत रखकर दुसरे को अगर K से गुणा किया जाये तो आयत का प्राप्त क्षेत्रफल K गुणा हो जायेगा |
☆ यदि किसी आयत के आसन्न भुजाओं में एक को शांत रखकर दुसरे को अगर K% से बढ़ाया जाये या फिर घटाया जाये, तो आयत का प्राप्त क्षेत्रफल भी K% से क्रमशः बढेगा या फिर घटेगा |

☆ आयत (Rectangle)

परिभाषा:- जिसकी आमने - सामने की भुजा आपस में बराबर हो, उसे आयत कहते है |
आयत का क्षेत्रफल = लम्बाई × चौड़ाई
आयत का परिमिति = 2 (लम्बाई + चौड़ाई)
आयत का विकर्ण = लम्बाई²+चौड़ाई²

 

आयत किसे कहते हैं

चार भुजाओं से घिरी वह आकृति, जिसमें आमने सामने की भुजाएँ समान्तर और बराबर हो तथा प्रत्येक कोण समकोण हो उसे आयत कहते हैं।

आयत

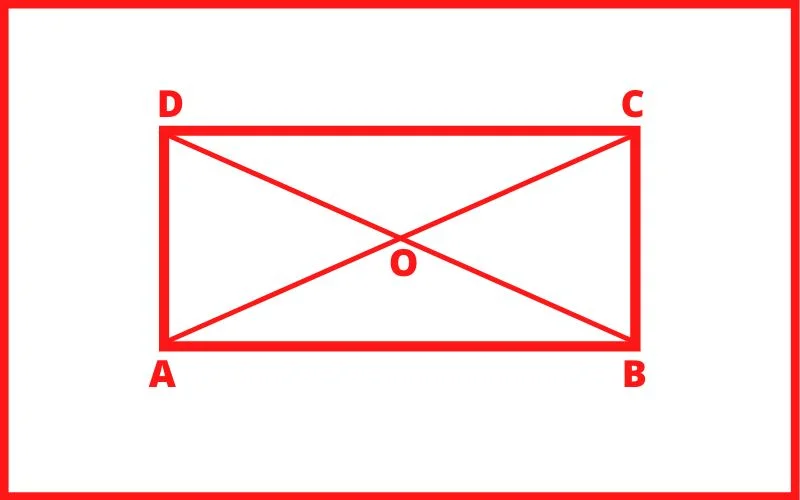
AC तथा BD को विकर्ण कहते हैं तथा ये आपस में बराबर होते हैं अर्थात AC = BD

आयत के सूत्र

आयत का परिमाप = 2(लम्बाई + चौड़ाई)
आयत का क्षेत्रफल = लंबाई ×चौड़ाई
आयत का विकर्ण =√(लंबाई² + चौड़ाई²)

आयत से सम्बंधित महत्वपूर्ण बिंदु

• जब किसी आयत में एक विकर्ण डाला जाए तो उसमें बने दो त्रिभुज के क्षेत्रफल समान होगें।
• जब आयत में दो विकर्ण डाले जाए तो दोनों की लम्बाई समान होगी और आमने सामने के कोण भी समान होगें।
• जब किसी आयत के अंदर बड़े से बड़े वृत्त को बनाया जाए तब आयत की चौड़ाई वृत्त के व्यास के बराबर होती हैं।
• अन्तः वृत्त का क्षेत्रफल (πb²/ 4) होता हैं।
• जब आयत के बाहर की तरफ वृत्त बना हो तब आयत का विकर्ण वृत्त के व्यास के बराबर होता हैं।

Case#1.

आयत की चौड़ाई = वृत का व्यास
चौड़ाई/2 = वृत्त की त्रिज्या
b/2 = r
r = b/2
दोनों पक्षों का वर्ग करके π से गुणा करने पर
πr² = π(b/2)²
आयत के अन्तः वृत्त का क्षेत्रफल = (πb²)/4

Case#2.

आयत के विकर्ण = वृत्त का व्यास
विकर्ण/2 = वृत्त की त्रिज्या
r = D/2
दोनों पक्षों का वर्ग करने पर
π r² = π (D/2)²
आयत के बाह्य वृत का क्षेत्रफल = (πD²)/4

Case#3.

आंतरिक वृत और बह्यवृत के अनुपातों का क्षेत्रफल
आंतरिक वृत : बह्यवृत
त्रिज्या का अनुपात = b : d
परिधि का अनुपात = b : d
क्षेत्रफल का अनुपात = b² : d²

Note :-

जब किसी आयत के अंतवृत और बाह्यवृत्त के संबंधों का अनुपात दर्शाया जाए।
त्रिज्या और परिधि के अनुपात हमेशा समान होगें, इनके वर्ग करने पर क्षेत्रफल का अनुपात प्राप्त हो।
आयत की चौथाई और विकर्ण ही अंतवृत और बह्यवृत की त्रिज्या और परिधि के अनुपात होते हैं।

In Sabhi Questions ko class me bataye gye formula & Concept se Krna h (only for Niharika and Priyanka SSC)

आयत के प्रश्न उत्तर

प्रश्न1. यदि किसी आयत की लम्बाई 5 सेंटीमीटर और चौड़ाई 7 सेंटीमीटर हो तो आयत का परिमाप क्या होगा?
A. 10 सेंटीमीटर
B. 14 सेंटीमीटर
C. 24 सेंटीमीटर
D. 28 सेंटीमीटर

हल:- दिया है.
लम्बाई a = 5 सेंटीमीटर
चौड़ाई b = 7 सेंटीमीटर
आयत का परिमाप = 2 (a + b)
P = 2 (5 + 7)
p = 2 × 12
P = 24 सेंटीमीटर
Ans. 24 सेंटीमीटर

प्रश्न2. यदि किसी आयत की लम्बाई एवं चौड़ाई क्रमशः 4 सेंटीमीटर और 12 सेंटीमीटर हो तो आयत का परिमाप क्या होगा?
A. 8 सेंटीमीटर
B. 16 सेंटीमीटर
C. 28 सेंटीमीटर
D. 32 सेंटीमीटर

हल:- दिया है.
लम्बाई a = 4 सेंटीमीटर
चौड़ाई b = 12 सेंटीमीटर
आयत का परिमाप = 2 (a + b)
P = 2 (4 + 12)
p = 2 × 16
P = 32 सेंटीमीटर
Ans. 32 सेंटीमीटर

प्रश्न3. यदि किसी आयत का परिमाप 24 सेंटीमीटर तथा लम्बाई 4 सेंटीमीटर हो, तो आयत की चौड़ाई निकालिए?
A. 8 सेंटीमीटर
B. 16 सेंटीमीटर
C. 32 सेंटीमीटर
D. 40 सेंटीमीटर

हल:- प्रश्नानुसार,
परिमाप = 24 सेंटीमीटर
लम्बाई = 4 सेंटीमीटर
आयत का परिमाप = 2 (लम्बाई + चौड़ाई)
24 = 2 (4 + चौड़ाई)
24/2 = 4 + चौड़ाई
12 = 4 + चौड़ाई
12 – 4 = चौड़ाई
चौड़ाई = 8 सेंटीमीटर

प्रश्न4. यदि किसी आयत का परिमाप 48 सेंटीमीटर तथा लम्बाई 12 सेंटीमीटर हो, तो आयत की चौड़ाई निकालिए?
A. 8 सेंटीमीटर
B. 16 सेंटीमीटर
C. 32 सेंटीमीटर
D. 40 सेंटीमीटर

हल:- प्रश्नानुसार,
परिमाप = 48 सेंटीमीटर
लम्बाई = 12 सेंटीमीटर
आयत का परिमाप = 2 (लम्बाई + चौड़ाई)
48 = 2 (12 + चौड़ाई)
48/2 = 12 + चौड़ाई
24 = 12 + चौड़ाई
24 – 12 = चौड़ाई
चौड़ाई = 12 सेंटीमीटर

प्रश्न5. यदि किसी आयत का परिमाप 32 सेंटीमीटर तथा चौड़ाई 8 सेंटीमीटर हो, तो आयत की लम्बाई निकालिए?
A. 2 सेंटीमीटर
B. 4 सेंटीमीटर
C. 6 सेंटीमीटर
D. 8 सेंटीमीटर

हल:- प्रश्नानुसार,
परिमाप = 32 सेंटीमीटर
चौड़ाई = 8 सेंटीमीटर
लम्बाई = ?
आयत का परिमाप = 2 (लम्बाई + चौड़ाई)
32 = 2 (लम्बाई + 8)
32/2 = लम्बाई + 8
16 = लम्बाई + 8
16 – 8 = लम्बाई
लम्बाई = 8 सेंटीमीटर
Ans. 8 सेंटीमीटर

प्रश्न6. यदि किसी आयत का परिमाप 56 सेंटीमीटर तथा चौड़ाई 18 सेंटीमीटर हो, तो आयत की लम्बाई निकालिए?
A. 8 सेंटीमीटर
B. 10 सेंटीमीटर
C. 12 सेंटीमीटर
D. 20 सेंटीमीटर

हल:- प्रश्नानुसार,
परिमाप = 56 सेंटीमीटर
चौड़ाई = 18 सेंटीमीटर
लम्बाई = ?
आयत का परिमाप = 2 (लम्बाई + चौड़ाई)
56 = 2 (लम्बाई + 18)
56/2 = लम्बाई + 18
28 = लम्बाई + 18
28 – 18 = लम्बाई
लम्बाई = 10 सेंटीमीटर
Ans. 10 सेंटीमीटर

प्रश्न7. एक आयताकार मैदान की लंबाई और चौड़ाई का अनुपात 4 : 3 हैं यदि मैदान का क्षेत्रफल 732 मीटर² हो तो मैदान के चारों और तीन बार लपेटने में कुल कितना तार लपेटना पड़ेगा?
A. 150 मीटर
B. 240 मीटर
C. 241 मीटर
D. 336 मीटर

हल:- आयताकार मैदान की लंबाई = 4x मीटर
तथा आयताकार मैदान की चौड़ाई = 3x मीटर
आयताकार मैदान का क्षेत्रफल = लम्बाई × चौड़ाई
768 = (4x) × (3x)
768 = 12 x²
x² = 768/12
x² = 64
x = √64
x = 8 मीटर
अतः लम्बाई = 4x
4 × 8 = 32 मीटर
तथा चौड़ाई = 3x
3 × 8 = 24 मीटर
आयताकार मैदान का परिमाप = 2 (लम्बाई + चौड़ाई)
= 2(32 + 24)
= 2 × 56
= 112 मीटर
अतः तीन चक्कर में लपेटा गया कुल तार = 3 × परिमाप
= 3 × 112
Ans. 336 मीटर

प्रश्न8. एक आयत की लम्बाई 15 सेंटीमीटर और इसके विकर्ण की लम्बाई 17 सेंटीमीटर हो तो आयत का क्षेत्रफल कितना होगा?
A. 120 वर्ग सेंटीमीटर
B. 220 वर्ग सेंटीमीटर
C. 60 वर्ग सेंटीमीटर
D. 180 वर्ग सेंटीमीटर

हल:- विकर्ण = 17 सेंटीमीटर
लम्बाई = 15 सेंटीमीटर
आयत का विकर्ण =√(l² + b²)
17 = √l² + (15)²
(17)² = l² + (15)²
(17)² – (15)² = l²
289 – 225 = l²
l² = 64
l = 8
आयत का क्षेत्रफल = l × b
= 8 × 15
Ans. 120 वर्ग सेंटीमीटर।

प्रश्न9. एक आयत का क्षेत्रफल 252 वर्ग सेंटीमीटर हैं। इसकी लम्बाई तथा चौड़ाई 9 : 7 हैं, इसका परिमाप क्या हैं?
A. 87 सेंटीमीटर
B. 56 सेंटीमीटर
C. 87 सेंटीमीटर
D. 64 सेंटीमीटर

हल:- आयत का क्षेत्रफल = 252
लम्बाई = 9
चौड़ाई = 7
9x × 7x = 252
63x² = 252
x² = 4
x = 2
9 × 2 = 18
7 × 2 = 14
आयत का परिमाप = 2(l + b)
= 2(18 + 14)
= 2 × 32
= 64
Ans. 64 सेंटीमीटर

प्रश्न10. एक आयताकार खेत के चारों और अंदर से सीमा से लगा हुआ 8 मीटर चौड़ा रास्ता बना हैं यदि खेत को लम्बाई और चौड़ाई क्रमशः 220 मीटर और 180 मीटर हो तो रास्ता का क्षेत्रफल क्या होगा?
A. 2,014 वर्ग मीटर
B. 3,024 वर्ग मीटर
C. 4,879 वर्ग मीटर
D. 6,144 वर्ग मीटर

हल:- क्षेत्रफल = लम्बाई × चौड़ाई
= 220 × 180
= 39,600 वर्ग मीटर
लम्बाई = 220 – 16
लम्बाई = 204
चौड़ाई = 180 – 16
चौड़ाई = 164
क्षेत्रफल = लम्बाई × चौड़ाई
= 204 × 164
= 33,456 वर्ग मीटर
रास्ते का क्षेत्रफल = 39,600 – 33,456
= 6,144
Ans. 6,144 वर्ग मीटर।

☆ वर्ग (Square)

परिभाषा:- जिसकी चारों भुजा आपस में बराबर हो, उसे वर्ग कहते है |
वर्ग का क्षेत्रफल = (भुजा) ²
वर्ग का परिमिति = 4 × भुजा
 

☆ त्रिभुज (Triangle)

परिभाषा:- तिन रेखाओं घेरे से घिरी हुई आकृति को त्रिभुज वर्ग कहते है |
त्रिभुज का क्षेत्रफल = 

12

 × आधार × ऊँचाई

☆ वृत (Circle)

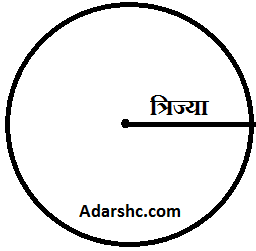परिभाषा:- गोल घेरे से घिरी हुई आकृति को वृत वर्ग कहते है |
वृत का क्षेत्रफल = π × (त्रिज्या)²
वृत की परिधि = 2π × त्रिज्या
वृत की त्रिज्या r = $\sqrt{\mathrm{<div\; class="frac"\; style="display:\; inline-block;\; letter-spacing:\; 0.001em;\; margin:\; 0px;\; padding:\; 0px;\; position:\; relative;\; text-align:\; center;\; vertical-align:\; middle;"><span\; style="display:\; block;\; margin:\; 0px;\; padding:\; 0.1em;">व्यास</span><span\; class="bottom"\; style="border-top:\; thin\; solid\; black;\; display:\; block;\; margin:\; 0px;\; padding:\; 0.1em;">2</span></div>}}$
वृत की त्रिज्या = 

वृत की परिधि2π

वृत का' व्यास = 

परिधिπ

☆ अर्द्ध-वृत (Semicircle)

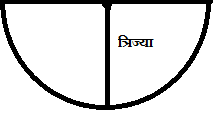परिभाषा:- गोल घेरे से घिरी हुई आकृति को वृत वर्ग कहते है |
अर्द्ध-वृत का क्षेत्रफल = 

12

 × πr²
अर्द्ध-वृत की परिमिति = πr या 

πd2

 जहाँ r = त्रिज्या और d = व्यास

☆ चतुर्भुज (Quadrilateral)

---

☆ समांतर चतुर्भुज (Parallelogram)

समांतर चतुर्भुज का क्षेत्रफल = आधार × ऊँचाई
समांतर चतुर्भुज का आधार = 

क्षेत्रफलऊँचाई

समांतर चतुर्भुज का ऊँचाई = 

क्षेत्रफलआधार

समांतर चतुर्भुज की परिमिति = 2 × (आसन्न भुजाओं का योग)

☆ समचतुर्भुज (Rhombus)

समचतुर्भुज का क्षेत्रफल = 1/2 × विकर्णों का गुणनफल

☆ समलम्ब चतुर्भुज

समलम्ब चतुर्भुज क्षेत्रफल = 1/2 × (समान्तर भुजाओं का योग) × उनके बीच की दूरी
विषमबाहु चतुर्भुज क्षेत्रफल = ½ (DP + BQ) × AC

☆ त्रिविमीय आकृतियाँ (Three dimensional Figures)

☆ घनाभ (Cuboid)

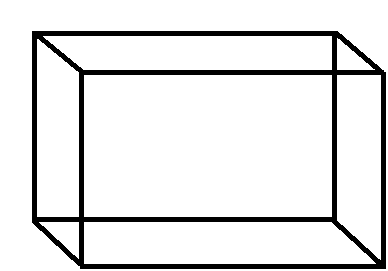यदि घनाभ की लम्बाई, चौड़ाई तथा ऊँचाई क्रमशः L, B और H हो तब घनाभ का आयतन = L × B × H
सम्पूर्ण पृष्ठ का क्षेत्रफल = 2 (L × B + B × H + H × L)

☆ घन (Cube)

यदि घन की प्रत्येक भुजा a हो, तब घन का आयतन = a × a × a = a³
सम्पूर्ण पृष्ठ का क्षेत्रफल = 6a²

☆ बेलन (Cylinder)

यदि बेलन की त्रिज्या r तथा ऊँचाई या लम्बाई h हो, तब बेलन का आयतन = πr²h
बेलन का वक्र पृष्ठ क्षेत्रफल = 2πrh
बेलन का सम्पूर्ण पृष्ठ का क्षेत्रफल = 2πr(h + r)

☆ शंकु (Cone)

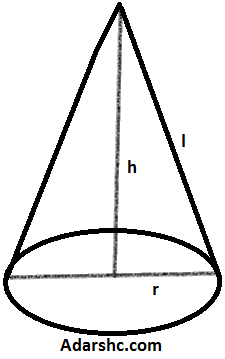यदि शंकु के आधार की त्रिज्या, ऊँचाई तथा इसकी तिर्यक-ऊँचाई क्रमशः r, h तथा ℓ हो, तब: शंकु का आयतन = 

13

 πr²h
शंकु वक्र-पृष्ठ का क्षेत्रफल = πrℓ
शंकु सम्पूर्ण पृष्ठ का क्षेत्रफल = πr(ℓ + r)

☆ गोला (Sphere)

यदि गोले की त्रिज्या r हो, तब आयतन = 

43

 πr³
गोला वक्र-पृष्ठ क्षेत्रफल = 4πr²

☆ अर्द्ध-गोला (Semisphere)

अर्द्ध-गोला का आयतन = 

23

πr²
अर्द्ध-गोला का वक्र-पृष्ठ क्षेत्रफल = 2πr²
अर्द्ध-गोला का सम्पूर्ण पृष्ठ क्षेत्रफल = 3πr²